Assignment 7, Q1-method 2

I am having difficulty getting method 1 to work properly but have completed this question using method 2. Please see a copy of my octave command and resulting images.

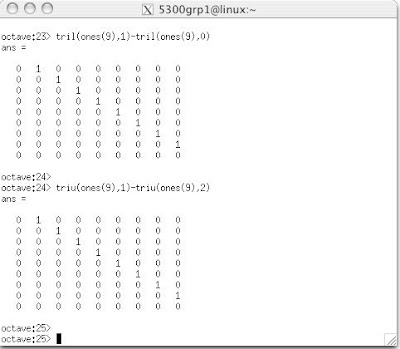
Please note that I created a "shrinkimg function" in octave and used it repeatedly to shrink my images by factors of 0.75, 0.25 and 0.1. Please click on the octave for more details as I have included # comments # to my code.



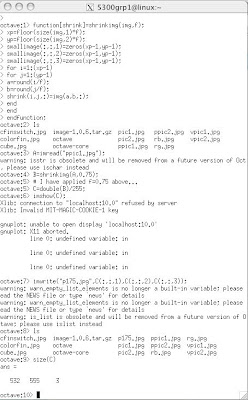
To use the function again you simply have to:

1) load your image - octave>A=imread("imagename.jpg");
2) apply shrink function - octave>B=shrinkimg(A, f); # f=0.75, 0.25, 0.1...
3) double your B - octave> C=double(B)/255;
4) then imwrite your new image C...

Here are my new images following the shrink function applied to my first picture.



Here are my new images following the shrink function applied to my second picture.

Assign 6, Q3c

Here is my first picture on the website:



Here are the commands I used to find the average colour and the subsequent colour 'chip' produced:





Please click on the octave picture for a 'closer view' of the code.

Here is the average colour chip and octave code of my second website image.







I have noticed that if there are a lot of different (major) colours present in a given image, then the less spectacular the colour chip becomes.

Example:

Assign 6, Q2

To create a 256x256 matrix with 1s in the (i, i+1) position and zeros everywhere else using the tril and/or triu functions in octave.

Here is what tril and triu mean:



Here are one line commands in octave that give you a 9x9 matrix with 1s in the (i,i+1) position and zeros everywhere else using the tril and triu command.



To make a 256x256 matrix with 1s in the (i,i+1) position and zeros everywhere else we simply write:

triu(ones(256),1)-triu(ones(256),2).

Assign #5, Q3bc

Just for fun...wanted to see how the rotation of bigT looked like without skewing by s=1 yet...

Here is the picture I got:



As you can see, the image is not very clear.

Applying a skewing factor first and then rotating the new image by pi/4, probably would not look very clear either. Here are the octave commands and resulting new image.